在 LevelDB 中，内存 MemTable 中的数据存储在 SkipList(跳表) 中，用来支持快速插入。跳表是 William Pugh 在论文 Skip Lists: A Probabilistic Alternative to Balanced Trees 中提出的一种概率性数据结构。有点类似有序链表，但是可以有多层，通过空间换时间，允许快速的查询、插入和删除操作，平均时间复杂度为 $ O(\log n) $。和一些平衡树比起来，代码实现也比较简单，性能稳定，因此应用比较广泛。

跳表实现的启发思路

那么跳表的原理是什么？LevelDB 中跳表又是怎么实现的呢？LevelDB 的跳表实现有哪些亮点以及优化呢？如何支持单线程写，并发读跳表呢？本文将从跳表的原理、实现等方面来深入探讨。最后还提供了一个可视化页面，可以直观看到跳表的构建以及整体结构。

跳表的原理

跳表主要用来存储有序的数据结构，在展开跳表的原理之前，先来看看在跳表之前，人们是怎么存储有序数据的。

存储有序数据

为了存储有序的抽象数据类型，最简单的方法是用有序二叉树，比如二叉搜索树（Binary Search Tree, BST）。在二叉搜索树中，每个节点包含一个键值，这个键值具有可比较性，允许执行有序操作。任何一个节点的左子树只包含键值小于该节点的键值的节点，而其右子树只包含键值大于该节点的键值的节点。

基于二叉搜索树的结构定义，我们很容易想到插入，查找操作的方法。比如查找的话，从树的根节点开始，逐级向下，如果目标键值小于当前节点的键值，则搜索左子树；如果目标键值大于当前节点的键值，则搜索右子树；如果相等，则找到了目标节点。插入也类似，找到目标后，在相应位置插入。删除操作稍微复杂，在找到目标节点后，需要根据当前节点的子树情况，来调整树的结构。这里不展开讲，感兴趣的话，可以去二叉搜索树可视化博客里面了解更多细节。

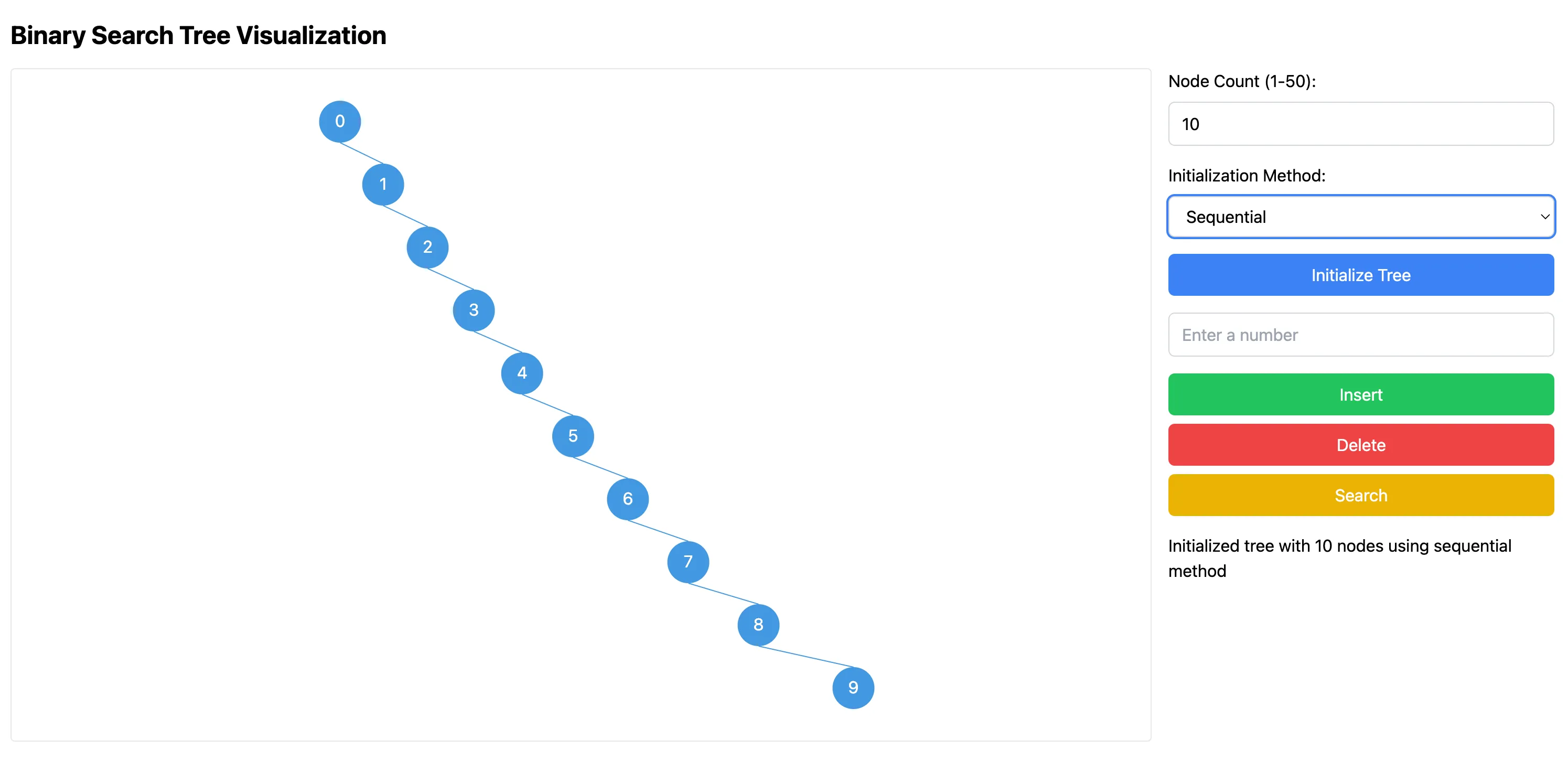
二叉搜索树的平均时间复杂度是 $ O(\log n) $，但如果二叉搜索树中的元素是按照顺序插入的，那么这棵树可能会退化成一个链表，使得操作的时间复杂度从 $ O(\log n) $ 退化为 $ O(n) $。比如下图就是按照顺序插入 10 个元素后，二叉搜索树的结构：

二叉搜索树退化为链表

顺便提下，可以在这里的可视化页面中更好理解这里的二叉搜索树。为了解决性能退化的问题，人们提出了很多平衡树，比如 AVL 树、红黑树等。这些平衡树的实现比较复杂，为了维护树的平衡性，增加了一些复杂的操作。

跳表的思想

上面的平衡树，都是强制树结构满足某个平衡条件，因此需要引入复杂的结构调整。跳表的作者，则另辟蹊径，引入了概率平衡而不是强制性的结构平衡。通过简单的随机化过程，跳表以较低的复杂性实现了与平衡树类似的平均搜索时间、插入时间和删除时间。

William Pugh 在论文中没有提到自己是怎么想到跳表思路的，只在 Related Work 中提到 Sprugnoli 在 1981 年提出了一种随机平衡搜索树。或许正是这里的随机思想启发了 Pugh，让他最终提出了跳表。其实随机思想还是挺重要的，比如 Google 提出的 Jumphash 一致性哈希算法，也是通过概率来计算应该在哪个 hash 桶，相比 hashring 方法有不少优点。

在开始跳表的原理之前，我们先回顾下有序链表的搜索。如果我们要查找一个有序链表，那么只能从头扫描，这样复杂度是 $ O(n) $。但这样就没有利用到有序的特性，如果是有序数组，通过二分查找，可以将复杂度降低到 $ O(\log n) $。有序链表和有序数组的差别就在于无法通过下标快速访问中间元素，只能通过指针遍历。

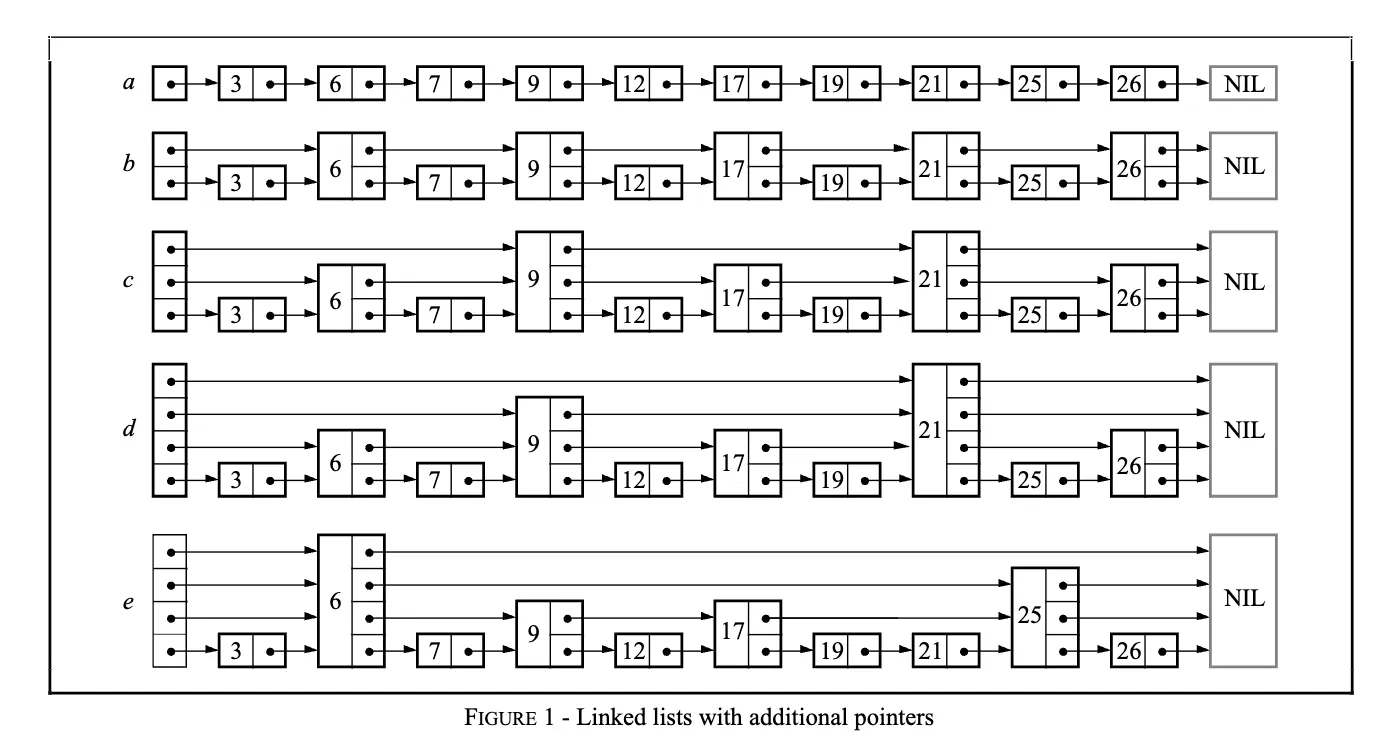
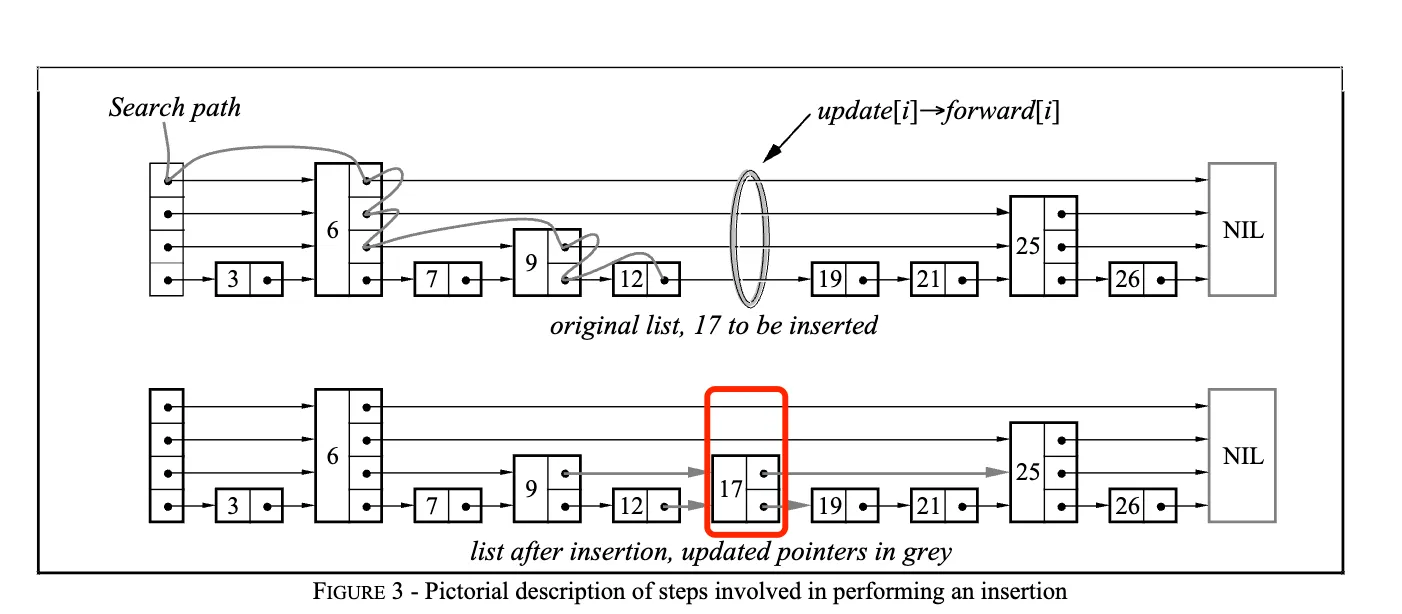
那么有什么办法可以让搜索的时候跳过一些节点，进而减少查找时间呢？一个比较直观的方法就是，创建多一点指针，用空间换时间。回到文章开始的图，$ a $是原始的有序链表，$ b $ 增加了些指针索引，可以 1 次跳 2 个，$ c $ 则进一步又增加了指针索引，可以1 次跳 4 个节点。

空间换时间，增加节点指针，加快查找速度

如果构建的链表中，每一层指针的节点数是下一层的 1/2，那么在最高层，只需要 1 次就能跳过一半的节点。在这种结构里查找的话，类似有序数组，可以通过二分查找的方式，快速定位到目标节点。因为整个链表索引高度是 $ O(\log n) $，查找的时间复杂度也是 $ O(\log n) $。

看起来很完美，只要我们不考虑插入和删除操作。如果要插入或者删除一个新节点，需要打乱并重构整个索引层，这是灾难性的。

跳表的作者 Pugh 为了解决这个问题，引入了随机化的思想，通过随机决定节点的层高，来避免插入和删除操作带来的复杂索引层重构。同时也用数学证明了，跳表的实现会保证平均时间复杂度是 $ O(\log n) $。

跳表的核心思想其实和上面的多层索引类似，通过多层索引来加速查找，每一层都是一个有序链表，最底层包含所有元素。每一层的节点都是前一层节点的子集，越往上层节点越稀疏。只是跳表的层高是随机决定的，不用像上面那样，每一层都是下一层的 1/2。因此插入和删除操作的代价是可控的，不会像多层索引那样，需要重构整个索引层。

当然跳表的实现还是有不少细节地方，下面通过 LevelDB 中的跳表实现来深入探讨。

LevelDB 中实现

LevelDB 中的跳表实现在 db/skiplist.h 中，主要是 SkipList 类，我们先来看看这个类的设计。

SkipList 类设计

SkipList 类定义了一个模板类，通过使用模板 template <typename Key, class Comparator>，SkipList 类可以用于任意数据类型的键（Key），并可以通过外部比较器（Comparator）自定义键的比较逻辑。这个 SkipList 只有 .h 文件，没有 .cc 文件，因为模板类的实现通常都在头文件中。 

1
2
3
4
5
6
7
8
9
10
11
12
13
template <typename Key, class Comparator>
class SkipList {
 private:
  struct Node;

 public:
  // Create a new SkipList object that will use "cmp" for comparing keys,
  // and will allocate memory using "*arena".  Objects allocated in the arena
  // must remain allocated for the lifetime of the skiplist object.
  explicit SkipList(Comparator cmp, Arena* arena);

  SkipList(const SkipList&) = delete;
  SkipList& operator=(const SkipList&) = delete;

SkipList 类的构造函数用于创建一个新的跳表对象，其中 cmp 是用于比较键的比较器，arena 是用于分配内存的 Arena 对象。SkipList 类通过 delete 禁用了拷贝构造函数和赋值运算符，避免了不小心复制整个跳表(没有必要，成本也很高)。

SkipList 类公开的核心操作接口有两个，分别是 Insert 和 Contains。Insert 用于插入新节点，Contains 用于查找节点是否存在。这里并没有提供删除节点的操作，因为 LevelDB 中 MemTable 的数据是只会追加的，不会去删除跳表中的数据。DB 中删除 key，在 MemTable 中只是增加一条删除类型的记录。

1
2
3
4
5
6
// Insert key into the list.
// REQUIRES: nothing that compares equal to key is currently in the list.
void Insert(const Key& key);

// Returns true iff an entry that compares equal to key is in the list.
bool Contains(const Key& key) const;

为了实现跳表功能，SkipList 类内部定义了 Node 类，用于表示跳表中的节点。之所以定义为内部类，是因为这样可以提高跳表的封装性和可维护性。

  • 封装性：Node 类是 SkipList 的实现的核心部分，但对于使用 SkipList 的用户来说，通常不需要直接与节点对象交互。将 Node 类定义为私有内部类可以隐藏实现细节；
  • 可维护性：如果跳表的实现需要修改或扩展，相关改动将局限于 SkipList 类的内部，而不会影响到外部使用这些结构的代码，有助于代码的维护和调试。

SkipList 类还有一些私有的成员和方法，用来辅助实现跳表的 Insert 和 Contains 操作。比如：

1
2
3
4
bool KeyIsAfterNode(const Key& key, Node* n) const;
Node* FindGreaterOrEqual(const Key& key, Node** prev) const;
Node* FindLessThan(const Key& key) const;
Node* FindLast() const;

此外，为了方便调用方遍历跳表，提供了一个公开的迭代器 Iterator 类。封装了常见迭代器的操作，比如 Next、Prev、Seek、SeekToFirst、SeekToLast 等。

接下来我们先看 Node 类的设计，然后分析 SkipList 如何实现插入和查找操作。最后再来看看对外提供的迭代器类 Iterator 的实现。

Node 节点类设计

Node 类是跳表中单个节点的表示，包含了节点的键值和多个层次的后继节点指针。有了这个类，SkipList 类就可以构建整个跳表了。先给出 Node 类的代码和注释，大家可以先品一品。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
template <typename Key, class Comparator>
struct SkipList<Key, Comparator>::Node {
  explicit Node(const Key& k) : key(k) {}

  Key const key;

  // Accessors/mutators for links.  Wrapped in methods so we can
  // add the appropriate barriers as necessary.
  Node* Next(int n) {
    assert(n >= 0);
    // Use an 'acquire load' so that we observe a fully initialized
    // version of the returned Node.
    return next_[n].load(std::memory_order_acquire);
  }
  void SetNext(int n, Node* x) {
    assert(n >= 0);
    // Use a 'release store' so that anybody who reads through this
    // pointer observes a fully initialized version of the inserted node.
    next_[n].store(x, std::memory_order_release);
  }

  // No-barrier variants that can be safely used in a few locations.
  Node* NoBarrier_Next(int n) {
    assert(n >= 0);
    return next_[n].load(std::memory_order_relaxed);
  }
  void NoBarrier_SetNext(int n, Node* x) {
    assert(n >= 0);
    next_[n].store(x, std::memory_order_relaxed);
  }

 private:
 // Array of length equal to the node height.  next_[0] is lowest level link.
  std::atomic<Node*> next_[1];
};

首先是成员变量 key，其类型为模板 Key，同时键是不可变的（const）。另外一个成员变量 next_ 在最后面，这里使用 std::atomic<Node*> next_[1]，来支持动态地扩展数组的大小。这就是C++ 中的柔性数组，next_ 数组用来存储当前节点的所有后继节点，next_[0] 存储最底层的下一个节点指针，next_[1] 存储往上一层的，以此类推。

在新建 Node 对象时，会根据节点的高度动态分配额外的内存来存储更多的 next 指针。SkipList 中封装了一个 NewNode 方法，这里提前给出代码，这样大家更好理解这里柔性数组对象的创建。

1
2
3
4
5
6
7
template <typename Key, class Comparator>
typename SkipList<Key, Comparator>::Node* SkipList<Key, Comparator>::NewNode(
    const Key& key, int height) {
  char* const node_memory = arena_->AllocateAligned(
      sizeof(Node) + sizeof(std::atomic<Node*>) * (height - 1));
  return new (node_memory) Node(key);
}

这里的代码平常见的少些，值得展开聊聊。首先计算 Node 需要的内存大小，Node 本身大小加上高度减 1 个 next 指针的大小，然后调用 Arena 的 AllocateAligned 方法分配内存。Arena 是 LevelDB 自己实现的内存分配类，详细解释可以参考LevelDB 源码阅读：内存分配器、随机数生成、CRC32、整数编解码。最后用 placement new 构造 Node 对象，这里主要是为了在 Arena 分配的内存上构造 Node 对象，而不是在堆上构造。

此外，Node 类还提供了 4 个方法，分别是 Next、SetNext、NoBarrier_Next 和 NoBarrier_SetNext，用来读取和设置下一个节点的指针。这里功能上只是简单的读取和设置 next_ 数组的值，但是用到了 C++ 的原子类型和一些同步语义，会在本文后面并发部分展开讨论。

Node 类先到这里，下面来看看 SkipList 中如何实现插入和查找操作。

跳表查找节点

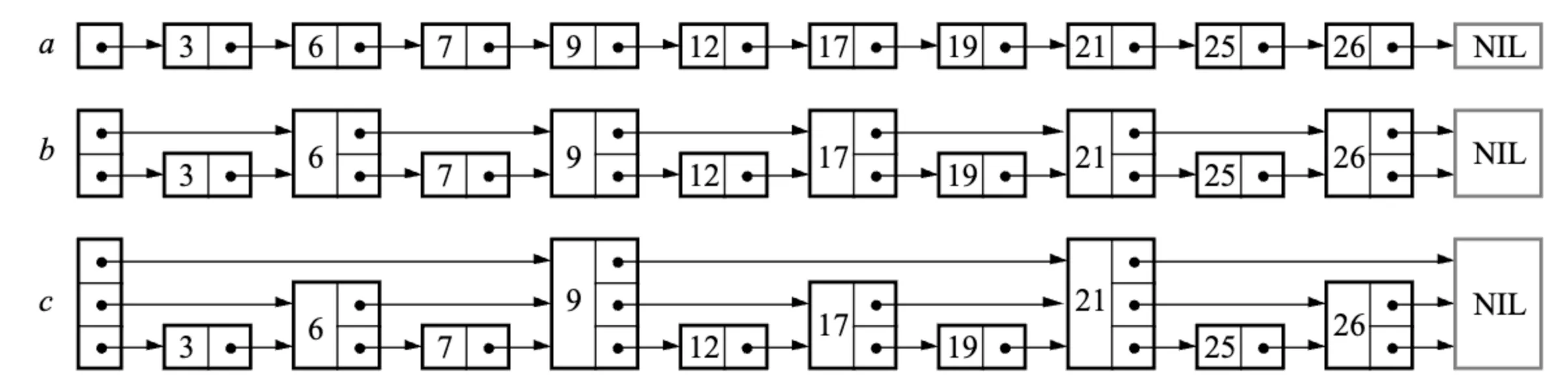
跳表中最基础的一个操作就是查找大于等于给定 key 的节点，在 SkipList 中为 FindGreaterOrEqual 私有方法。跳表对外公开的检查是否存在某个 key 的 Contains 方法，就是通过它来实现的。在插入节点的，也会通过这个方法来找到需要插入的位置。在看 LevelDB 中具体实现代码前，可以先通过论文中的一张图来理解这里的查找过程。

跳表查找节点过程

查找过程从跳表当前最高层开始往右、往下进行搜索。实现中为了简化一些边界检查，一般添加一个哑元节点作为头部节点，不存储具体数值。查找时，首先初始化当前节点为头节点 head_，然后从最高层开始往右搜索，如果同一层右边的节点的 key 小于目标 key，则继续向右搜索；如果大于等于目标 key，则向下一层搜索。循环这个查找过程，直到在最底层找到大于等于目标 key 的节点。

接下来看看 FindGreaterOrEqual 的具体实现代码，代码简洁，逻辑也很清晰。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// Return the earliest node that comes at or after key.
// Return nullptr if there is no such node.
//
// If prev is non-null, fills prev[level] with pointer to previous
// node at "level" for every level in [0..max_height_-1].
template <typename Key, class Comparator>
typename SkipList<Key, Comparator>::Node*
SkipList<Key, Comparator>::FindGreaterOrEqual(const Key& key,
                                              Node** prev) const {
  Node* x = head_;
  int level = GetMaxHeight() - 1;
  while (true) {
    Node* next = x->Next(level);
    if (KeyIsAfterNode(key, next)) {
      // Keep searching in this list
      x = next;
    } else {
      if (prev != nullptr) prev[level] = x;
      if (level == 0) {
        return next;
      } else {
        // Switch to next list
        level--;
      }
    }
  }
}

这里值得一说的是 prev 指针数组，用来记录每一层的前驱节点。这个数组是为了支持插入操作，插入节点时，需要知道新节点在每一层的前驱节点，这样才能正确地插入新节点。这里的 pre 数组是通过参数传递进来的，如果调用者不需要记录搜索路径，可以传入 nullptr。

有了这个方法，很容易就能实现 Contains 和 Insert 方法了。Contains 方法只需要调用 FindGreaterOrEqual，然后判断返回的节点是否等于目标 key 即可。这里不需要前驱节点，所以 prev 传入 nullptr 即可。

1
2
3
4
5
6
7
8
9
template <typename Key, class Comparator>
bool SkipList<Key, Comparator>::Contains(const Key& key) const {
  Node* x = FindGreaterOrEqual(key, nullptr);
  if (x != nullptr && Equal(key, x->key)) {
    return true;
  } else {
    return false;
  }
}

跳表插入操作

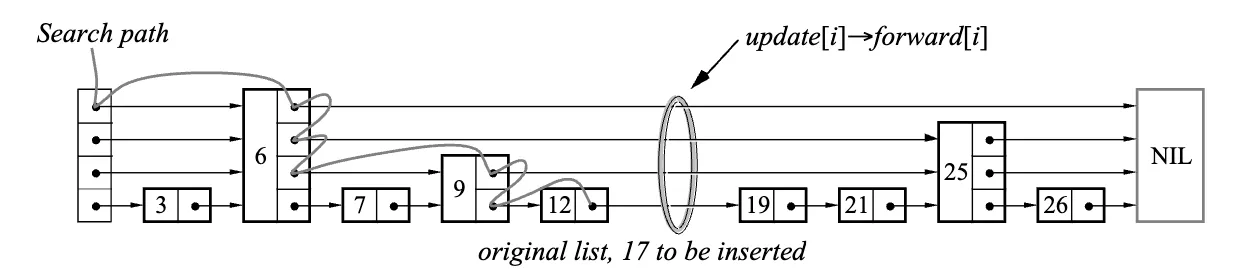
插入节点相对复杂些，在看代码之前，还是来看论文中给出的图。上半部分是查找要插入位置的逻辑，下面是插入节点后的跳表。这里看到增加了一个新的节点，然后更新了指向新节点的指针，以及新节点指向后面节点的指针。

跳表插入节点过程

那么新插入节点的高度是多少？插入相应位置后，前后节点的指针又是怎么更新的呢？来看看 LevelDB 中的实现代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
template <typename Key, class Comparator>
void SkipList<Key, Comparator>::Insert(const Key& key) {
  Node* prev[kMaxHeight];           // 1
  Node* x = FindGreaterOrEqual(key, prev);

  // Our data structure does not allow duplicate insertion
  assert(x == nullptr || !Equal(key, x->key));

  int height = RandomHeight();      // 2
  if (height > GetMaxHeight()) {
    for (int i = GetMaxHeight(); i < height; i++) {
      prev[i] = head_;
    }
    max_height_.store(height, std::memory_order_relaxed);
  }

  x = NewNode(key, height);         // 3
  for (int i = 0; i < height; i++) {
    x->NoBarrier_SetNext(i, prev[i]->NoBarrier_Next(i));
    prev[i]->SetNext(i, x);
  }
}

上面代码省略掉了部分注释，然后分为 3 个功能块，下面是每一部分的解释：

  1. 首先定义一个类型为 Node*的数组 prev，长度为跳表的最大支持层高 kMaxHeight=12。这个数组存储要插入的新节点每一层的前驱节点，在跳表中插入新节点时，可以通过这个 pre 数组找到新节点在每一层插入的位置。
  2. 通过随机算法，来决定新节点的层高 height。这里 LevelDB 初始层高为 1，然后以 1/4 的概率决定是否增加一层。如果新节点的高度超过了当前跳表的最大高度，需要更新最大高度，并将超出的部分的 prev 设置为头节点，因为新的层级是从头节点开始的。
  3. 创建一个高度为 height 的新节点，并插入在链表中。具体做法也很简单，遍历新节点的每一层，使用 NoBarrier_SetNext 方法来设置新节点的下一节点，接着更新 prev 节点的下一节点为新节点，实现了新节点的插入。NoBarrier_SetNext 说明在这个上下文中，不需要额外的内存屏障来保证内存操作的可见性。新节点插入和一般链表的插入操作区别不大，这里有个不错的可视化，可以加深对链表的插入理解。

下面来看看其中的部分细节。首先来看看 RandomHeight 方法，这个方法用来生成新节点的高度，核心代码如下：

1
2
3
4
5
6
7
8
9
10
template <typename Key, class Comparator>
int SkipList<Key, Comparator>::RandomHeight() {
  // Increase height with probability 1 in kBranching
  static const unsigned int kBranching = 4;
  int height = 1;
  while (height < kMaxHeight && rnd_.OneIn(kBranching)) {
    height++;
  }
  return height;
}

这里 rnd_ 是一个 Random 对象，是 LevelDB 自己的线性同余随机数生成器类，详细解释可以参考LevelDB 源码阅读：内存分配器、随机数生成、CRC32、整数编解码。RandomHeight 方法中，每次循环都会以 1/4 的概率增加一层，直到高度达到最大支持高度 kMaxHeight=12 或者不满足 1/4 的概率。这里总的层高 12 和概率值 1/4 是一个经验值，论文里面也提到了这个值，后面在性能分析部分再来讨论这两个值的选择。

这里插入链表其实需要考虑并发读问题，不过在这里先不展开，后面会专门讨论。接下来先看看 SkipList 中的迭代器类 Iterator 的设计。

Iterator 迭代器

Iterator 迭代器类主要用于遍历跳表中的节点。这里迭代器的设计和用法也比较有意思，LevelDB 在 include/leveldb/iterator.h 中，定义了一个抽象基类 leveldb::Iterator ，里面有通用的迭代器接口，可以用于不同的数据结构。

而这里 SkipList<Key, Comparator>::Iterator 是 SkipList 的内部类，定义在 db/skiplist.h 中，只能用于 SkipList 数据结构。跳表的 Iterator 并没有继承 leveldb::Iterator 抽象基类，而是作为 MemTableIterator 对象的成员被组合使用。具体是用在 db/memtable.cc 中，这里定义了 MemTableIterator 类，继承自 Iterator，然后用跳表的 Iterator 重写了其中的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
class MemTableIterator : public Iterator {
 public:

  void SeekToLast() override { iter_.SeekToLast(); }
  void Next() override { iter_.Next(); }
  void Prev() override { iter_.Prev(); }
  // ...
  Status status() const override { return Status::OK(); }

 private:
  MemTable::Table::Iterator iter_;
  std::string tmp_;  // For passing to EncodeKey
};

这里 MemTableIterator 充当了适配器的角色，将 SkipList::Iterator 的功能适配为符合 LevelDB 外部 Iterator 接口的形式，确保了 LevelDB 各部分间接口的一致性。如果未来需要替换 memtable 中的跳表实现或迭代器行为，可以局部修改 MemTableIterator 而不影响其他使用 Iterator 接口的代码。

那么 SkipList::Iterator 类具体怎么定义的呢？如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// Iteration over the contents of a skip list
  class Iterator {
   public:
    // Initialize an iterator over the specified list.
    // The returned iterator is not valid.
    explicit Iterator(const SkipList* list);

    // Returns true iff the iterator is positioned at a valid node.
    bool Valid() const;

    // Returns the key at the current position.
    const Key& key() const;

    void Next();
    void Prev();

    // Advance to the first entry with a key >= target
    void Seek(const Key& target);

    // Position at the first entry in list.
    // Final state of iterator is Valid() iff list is not empty.
    void SeekToFirst();

    // Position at the last entry in list.
    // Final state of iterator is Valid() iff list is not empty.
    void SeekToLast();

   private:
    const SkipList* list_;
    Node* node_;
    // Intentionally copyable
  };

通过传入 SkipList 指针对象，就可以遍历跳表了。类中定义了 Node* node_ 成员变量，用来记录当前遍历到的节点。大部分方法实现起来都不难，稍微封装下前面介绍过的跳表中的方法就行。有两个方法比较特殊，需要在跳表中增加新的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template <typename Key, class Comparator>
inline void SkipList<Key, Comparator>::Iterator::Prev() {
  // Instead of using explicit "prev" links, we just search for the
  // last node that falls before key.
  assert(Valid());
  node_ = list_->FindLessThan(node_->key);
  if (node_ == list_->head_) {
    node_ = nullptr;
  }
}

template <typename Key, class Comparator>
inline void SkipList<Key, Comparator>::Iterator::SeekToLast() {
  node_ = list_->FindLast();
  if (node_ == list_->head_) {
    node_ = nullptr;
  }
}

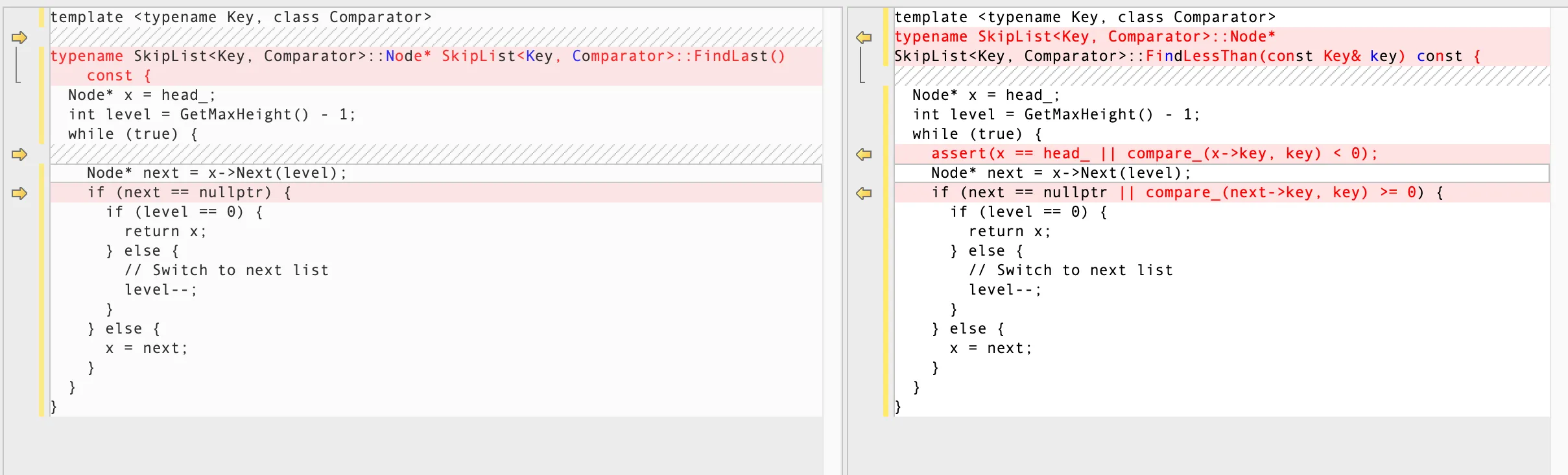
这里分别调用跳表的 FindLessThan 和 FindLast 方法，来实现 Prev 和 SeekToLast 方法。其中 FindLessThan 查找小于给定键 key 的最大节点，FindLast 查找跳表中的最后一个节点（即最大的节点）。这两个方法本身很相似，和 FindGreaterOrEqual 方法也很类似，如下图列出这两个方法的区别。

跳表查找方法FindLessThan和FindLast区别

基本思路就是从跳表的头节点开始，逐层向右、向下查找。在每一层，检查当前节点的下一个节点是否存在。如果下一个节点不存在，则切换到下一层继续查找。存在的话，则需要根据情况判断是否向右查找。最后都是到达最底层（第0层），返回某个节点。

至此，跳表的核心功能实现已经全部梳理清楚了。不过还有一个问题需要回答，在多线程情况下，这里跳表的操作是线程安全的吗？上面分析跳表实现的时候，有意忽略了多线程问题，接下来详细看看。

并发读问题

我们知道 LevelDB 虽然只支持单个进程使用，但是支持多线程。更准确的说，在插入 memtable 的时候，LevelDB 会用锁保证同一时间只有一个线程可以执行跳表的 Insert 操作。但是允许有多个线程并发读取 SkipList 中的数据，这里就涉及到了多线程并发读的问题。这里 LevelDB 是怎么支持一写多读的呢？

在 Insert 操作的时候，改动的数据有两个，一个是整个链表当前的最大高度 max_height_，另一个是插入新节点后导致的节点指针更新。虽然写入过程是单线程的，但是最大高度和 next 指针的更新这两个操作并不是原子的，并发读的线程可能读到旧的 height 值或者未更新的 next 指针。我们看 LevelDB 具体是怎么解决这里的问题的。

在插入新节点时，先读链表当前最大高度，如果新节点更高，则需要更新最大高度。当前链表最大高度是用原子类型 std::atomic 记录的，用 std::memory_order_relaxed 语义保证了对 max_height_ 的读写操作是原子的，但是没有增加内存屏障。相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline int GetMaxHeight() const {
  return max_height_.load(std::memory_order_relaxed);
}

template <typename Key, class Comparator>
void SkipList<Key, Comparator>::Insert(const Key& key) {
  // ...
  if (height > GetMaxHeight()) {
    for (int i = GetMaxHeight(); i < height; i++) {
      prev[i] = head_;
    }
    max_height_.store(height, std::memory_order_relaxed);
  }
  // ... 后续设置节点指针 (这里可能发生指令重排)

对于读的线程来说，如果读到一个新的高度值和更新后的节点指针，这是没有问题的，读线程正确感知到了新的节点。但是如果写线程还没来的及更新完节点指针，这时候读线程读到新的高度值，会从新的高度开始查找，不过此时 head_->next[max_height_] 指向 nullptr，因此会往下继续查找，也不会影响查找过程。其实这种情况，如果写线程更新了下面层次的指针，读线程也有可能会感知到新的节点的存在。

另外，会不会出现写线程更新了新节点指针，但是读线程读到了老的高度呢？我们知道，编译器和处理器可能会对指令进行重排，只需要保证这种重排不违反单个线程的执行逻辑。上面写操作，可能在更新完节点指针后，才写入 max_height_。这时候读线程读到老的高度值，它没感知到新添加的更高层级，查找操作仍然可以在现有的层级中完成。其实这时候对读线程来说，它感知到的是多了一个层级较低的新的节点。

Node 内存屏障

其实前面分析还忽略了一个重要的地方，那就是层级指针更新时候的并发读问题。前面我们假设新节点层级指针更新的时候，写线程从下往上一层层更新，读线程可能读到部分低层级指针，但不会读到不完整的层级指针。为了高效实现这点，LevelDB 使用了内存屏障，这要从 Node 类的设计说起。

在上面的 Node 类实现中，next_ 数组使用了 atomic 类型，这是 C++11 中引入的原子操作类型。Node 类还提供了两组方法来访问和更新 next_ 数组中的指针。Next 和 SetNext 方法是带内存屏障的，内存屏障的的主要作用：

  1. 防止重排序：确保在内存屏障之前的所有写操作都在内存屏障之后的操作之前完成。
  2. 可见性保证：确保在内存屏障之前的所有写操作对其他线程可见。

具体到这里，SetNext 方法使用了 atomic 的 store 操作，并指定了内存顺序 memory_order_release，它提供了以下保证：在这个 store 之前的所有写操作都会在这个 store 之前完成，这个 store 之后的所有读操作都会在这个 store 之后开始。读线程用的 Next 方法使用 memory_order_acquire 来读取指针，确保在读操作之后发生的读或写操作不会被重排序到加载操作之前。

NoBarrier_Next 和 NoBarrier_SetNext 方法则是不带内存屏障的，这两个方法使用 memory_order_relaxed，编译器不会在这个操作和其他内存操作之间插入任何同步或屏障，因此不提供任何内存顺序保证，这样会有更高的性能。

背景就先介绍到这里，有点绕，没关系，下面结合代码来看看：

1
2
3
4
5
6
7
x = NewNode(key, height);
for (int i = 0; i < height; i++) {
  // NoBarrier_SetNext() suffices since we will add a barrier when
  // we publish a pointer to "x" in prev[i].
  x->NoBarrier_SetNext(i, prev[i]->NoBarrier_Next(i)); // 后驱指针
  prev[i]->SetNext(i, x); // 前驱指针
}

这段代码从下往上更新新节点的层级指针。对于第 i 层，只要写线程执行完 SetNext(i, x)，修改了这一层指向新节点 x 的指针，那么其他读线程就能看到完整初始化的第 i 层。这里要理解完整初始化的含义，我们可以假设这里没有内存屏障，那么会出现什么情况呢？

  • 不一致的多层指针：不同层级的指针可能会以不一致的顺序被更新，读线程可能会看到高层指针已更新，但低层指针还未更新的情况。
  • 内存可见性问题：在多核系统中，一个核心上的写操作可能不会立即对其他核心可见，导致其他线程可能会长时间看不到新插入的节点。
  • 节点指针错乱：这里先更新了指向新节点的指针，但是没有更新新节点的后驱指针。导致读线程读到新节点后，没有后驱指针，以为读到了结尾。

有内存屏障后，这里就保证了从下往上，每一层都是完整的初始化状态。LevelDB 这里也是优化到了极致，减少了不必要的内存屏障。在 i 层插入节点 x 时，需要同时更新 x 的后驱和前驱指针，对于后驱指针，使用 NoBarrier_SetNext 方法就足够了，因为在后续设置前驱指针的时候，会使用 SetNext 添加内存屏障。这里代码中的注释也提到了这点。

跳表在线可视化

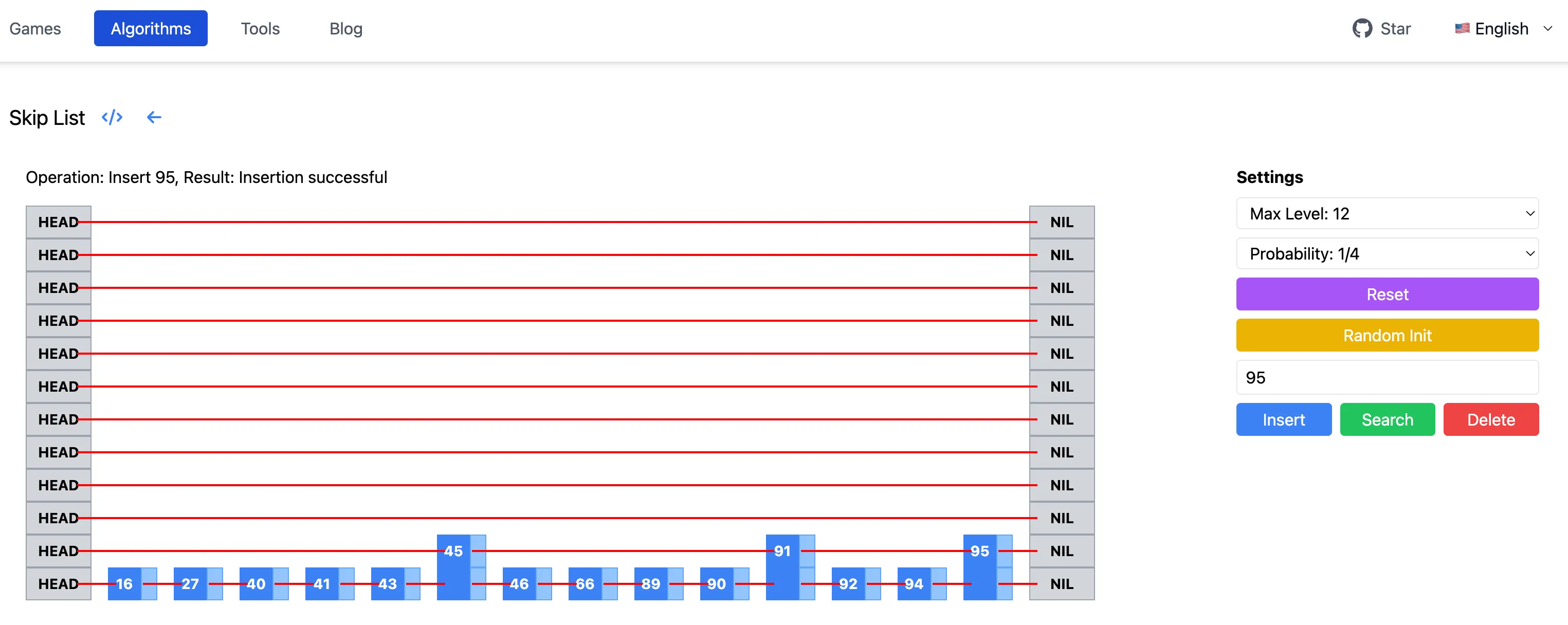
为了直观看看跳表构建的过程，我用 Claude3.5 做了一个跳表可视化页面。可以指定跳表的最大层高，以及调整递增层高的概率，然后可以随机初始化跳表，或者插入、删除、查找节点，观察跳表结构的变化。

跳表在线可视化

在最高 12 层，递增概率为 1/4 的情况下，可以看到跳表平均层高还是挺低的。这里也可以调整概率为 1/2，看看跳表的变化。

总结

跳表是一种概率性数据结构，可以用来替代平衡树，实现了快速的插入、删除和查找操作。LevelDB 中的跳表实现代码简洁，性能稳定，适合用来存储内存 MemTable 中的数据。本文从跳表的原理、实现等方面来深入探讨，最后还提供了一个可视化页面，可以直观看到跳表的构建过程。

LevelDB 的一大优点就是提供了详细的测试，那么跳表这里又是怎么测试的呢？另外，通过引入随机化，跳表性能和平衡树差不多，我们怎么来分析跳表的性能呢？下篇见～