LevelDB 源码阅读:如何分析跳表的时间复杂度?
0 Comment在上篇 LevelDB 源码阅读:跳表的原理、实现以及可视化中,详细分析了 LevelDB 中跳表的实现。然后在 LevelDB 源码阅读:如何正确测试跳表的并行读写? 中,分析了 LevelDB 跳表的测试代码,最后还剩下一个问题,怎么分析跳表的时间复杂度呢?
在分析完跳表的时间复杂度之后,就能明白 LevelDB 中概率值和最大高度的选择,以及 Redis 为什么选择不同的最大高度。最后本文也会提供一个简单的压测代码,来看看跳表的性能如何。
本文不会有很高深的数学知识,只涉及简单的概率论,可以放心往下看。跳表的性能分析有不少思路很值得借鉴,希望本文能抛砖引玉,给大家带来一些启发。
跳表性能分析拆解
在知道 LevelDB 的原理和实现后,我们可以推测出来,在极端情况下,每个节点的高度都是 1,那么跳表的查找、插入、删除操作的时间复杂度都会退化到 O(n)。在这种情况下,性能比平衡树差了不少。当然,因为有随机性在里面,所以没有输入序列能始终导致性能最差。
那么跳表的平均性能如何呢?前面给出过结论,和平衡树的平均性能差不多。引入一个简单的随机高度,就能保证跳表的平均性能和平衡树差不多。这背后有没有什么分析方法,能够分析跳表的性能呢?
还得看论文,论文中给出了一个不错的分析方法,不过这里的思路其实有点难想到,理解起来也有点费劲。我会把问题尽量拆分,然后一步步来推导整个过程,每一步涉及到的数学推导也尽量给出来。哈哈,这不就是思维链嘛,拆解问题并逐步推理,是人和 AI 解决复杂问题的必备技能啊。这里的推导可以分为几个小问题:
- 跳表的查找、插入和删除操作,哪部分操作最影响耗时?
- 对于查找操作,假设从任意层 k 开始往下找,这里的平均复杂度是多少(遍历多少次)?
- 有没有什么办法,可以在链表中找到某个层数,从这层开始查找效率最高,并且遍历次数能代表平均性能?
- 能不能找到一个公式,来计算总的时间复杂度,并算出这里的平均复杂度上限?
好了,下面我们逐个问题分析。
跳表操作瓶颈
第一个小问题比较简单。在前文讲跳表的原理和实现中,我们知道,对于插入和删除操作,也需要先通过查找操作找到对应的位置。之后就是几个指针操作,代价都是常量时间,可以忽略。所以,跳表操作的时间复杂度就是看查找操作的复杂度。
查找操作的过程就是往右,往下搜索跳表,直到找到目标元素。如果我们能知道这里搜索的平均复杂度,那么就可以知道跳表操作的平均复杂度。直接分析查找操作的平均复杂度,有点无从下手。按照 LevelDB 里面的实现,每次是从当前跳表中节点的最高层数开始找。但是节点高度是随机的,最高层数也是随机的,似乎没法分析从随机高度开始的查找操作的平均复杂度。
跳 k 层的期望步数
先放弃直接分析,来尝试回答前面第二个问题。假设从任意层 k 开始往下找,平均要多少次才能找到目标位置呢?这里的分析思路比较跳跃,我们反过来分析从目标位置,往上往左查找,平均要多少步才能往上查 k 层。并且假设链表中节点高度是在反向查找过程中,根据概率 p 来随机决定的。
这种假设和分析过程得到的平均查找次数和真实查找情况等价吗?我们知道往右往下执行查找的时候,节点的高度都是已经决定的了。但是考虑到节点的高度本来就是随机决定的,假设反向查找时候来决定高度,并且逆向整个搜索过程,在统计上没有什么不同。
接下来我们假设当前处在节点 x 的任意一层 i (下图中的情形 a),从这个位置往上查 k 层置需要 步。我们不知道节点 x 上面还有没有层,也不知道节点 x 的左边还有没有节点(下图中用阴影问号表示这种未知)。再假设 x 不是 header 节点,左边还有节点(其实这里分析的话可以假设左边有无穷多节点)。
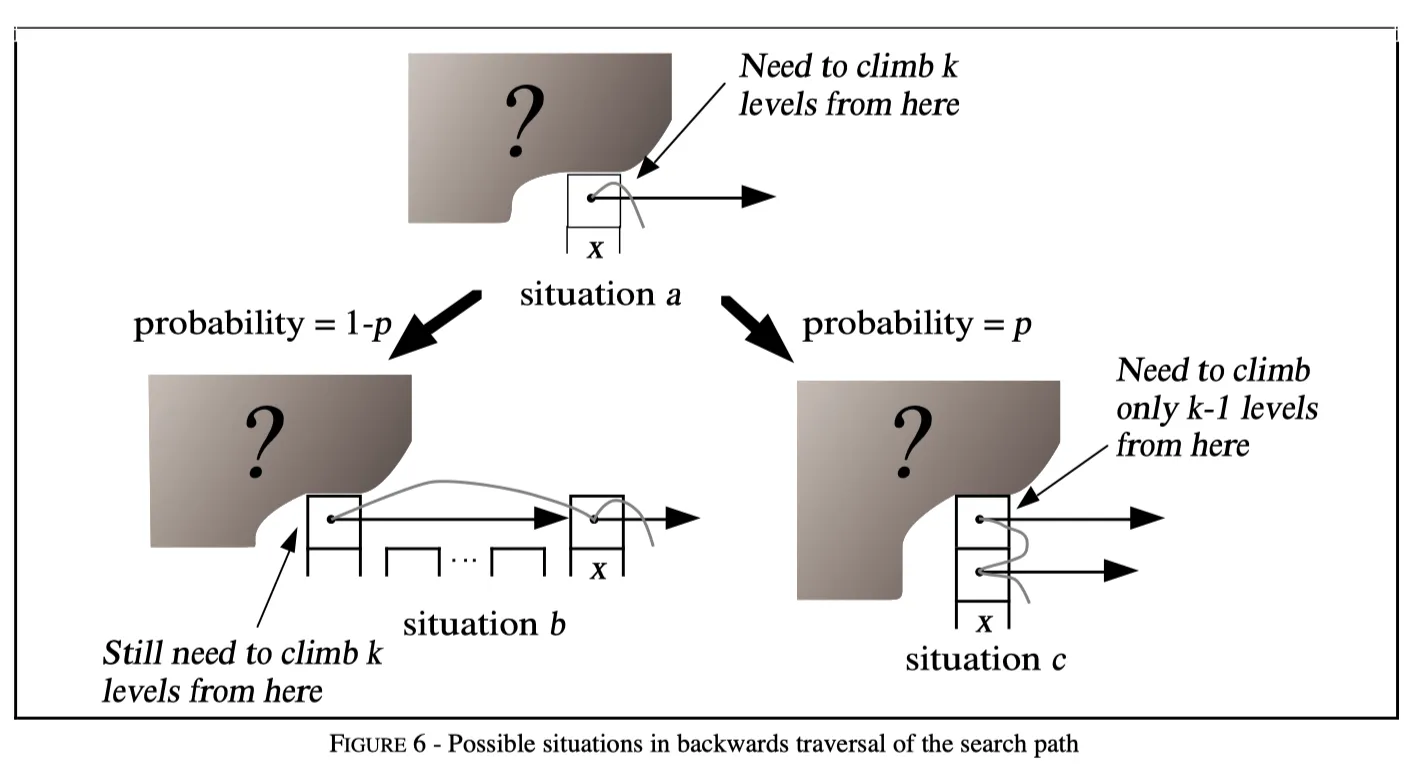 LevelDB 时间复杂度分析从 K 层查找复杂度(图片来自论文)
LevelDB 时间复杂度分析从 K 层查找复杂度(图片来自论文)
那么整个链表的节点情况有两种可能,整体如上图:
- 情形 b: 节点 x 一共就是 i 层,在左边有节点,查找的时候需要从左边节点的第 i 层水平跳到 x 的第 i 层。逆向分析的话,因为按照 的概率决定是否有更高层,所以这里处于情形 b 的概率是 。然后左边节点和 x 在同一层,往上查 k 层仍然需要 步。因此这种情况下期望的查找步数是: 。
- 情形 c: 节点 x 层高大于 i,那么查找的时候需要从 x 的第 i+1 层往下跳到第 i 层。逆向分析的话,因为按照 的概率决定是否有更高层,所以这里处于情形 c 的概率是 。然后从 i+1 层往上查 k 层,等价于从第 i 层往上查找 k-1 层,需要 步。因此期望的查找步数是: 。
也就是说,对于从任意层 i 开始查找,往上跳 层需要的期望步数为:
化简这个方程得到下面结果:
这里从任意层 i 开始查找往上跳 k 层需要的期望步数 ,也等价于从第 k 层开始正常步骤查找,到最底层目标位置需要的期望步数。这个公式很重要,只要理解了这里的逆向分析步骤,最后公式也比较好推导出来。但是用这个公式还是没法直接分析出跳表的平均性能,中间缺少了点什么。
从哪层开始搜索?
从上面分析可以看到从第 K 层查找到底层的时间复杂度是 ,那么实际跳表查找的时候,从哪层开始搜索比较好呢?在LevelDB 源码阅读:跳表的原理、实现以及可视化可以知道跳表中节点的层高是随机的,对于其中某层,可能有多个节点,越往上层,节点数越少。
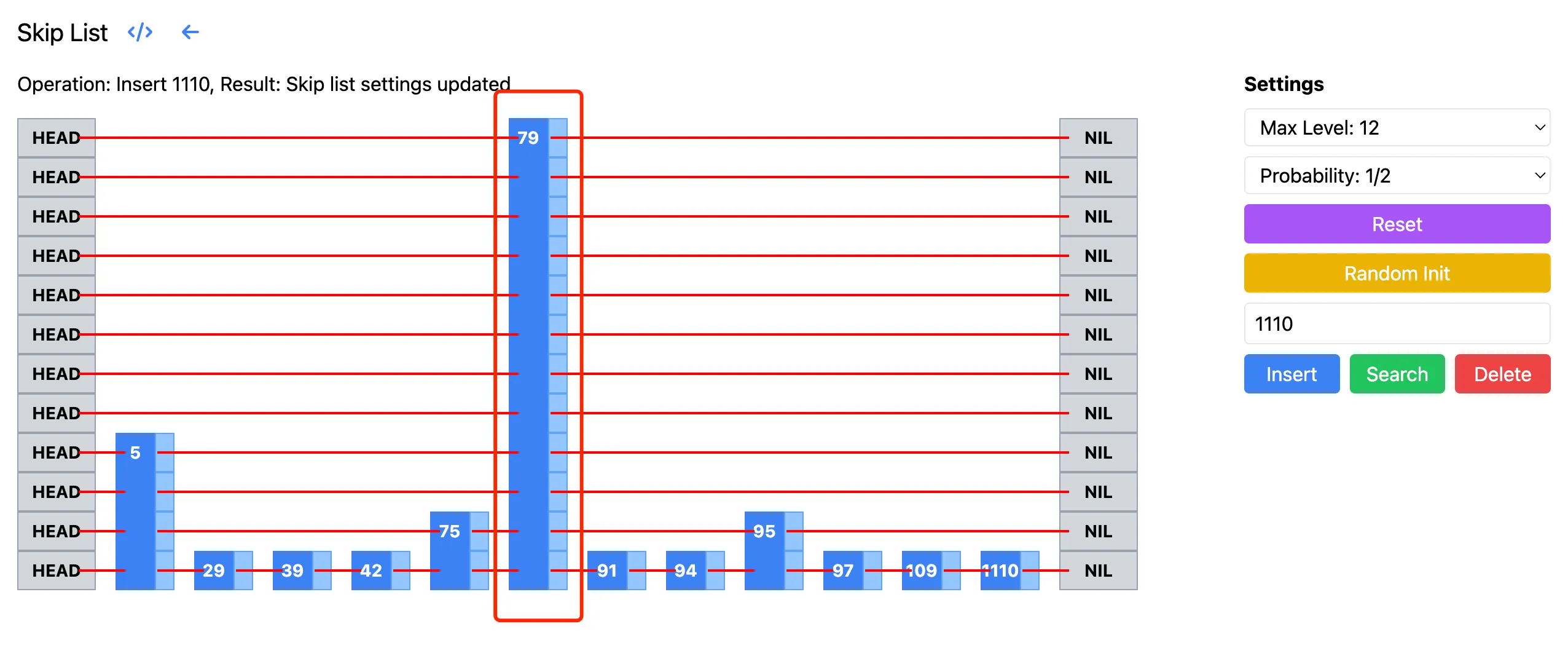
LevelDB 的实现中,是从跳表的最高层开始查找的。但其实如果从最高层开始搜索,可能会做很多无用功。比如下面的跳表中,其中 79 对应的层非常高,从这层开始搜索,需要往下走很多步,都是无效搜索。如果从 5 对应的层高开始搜索,则节省了不少搜索步骤。下图来自跳表的可视化页面:
理想情况下,我们希望从一个”合适“的层级开始搜索。论文中是这样定义合适的层:在该层期望看到 个节点。因为我们的 p 一般取值 1/2,1/4 这样的值,所以这里一般从有 2 或者 4 个节点的层开始搜索。从这个层开始搜索,不至于做无用功,也不至于从太低层开始的话,失去跳表的优势。接下来只需要知道这样的层,平均有多高,然后结合前面的 就可以知道整体的搜索复杂度了。
层高推算
现在来看看具体的推算步骤。假设一共有 个节点,然后在第 层有 个节点。因为每次以 的概率决定是否向上层跳,所以有:
注意 L 层跳 次,所以这里的 是 L-1 次幂。将等式两边同时乘以 p:
然后两边取对数 ,如下,这里用到了对数的乘法法则和幂法则:
接着进行简化:
所以我们得到:
也就是说,在 层,期望有 个节点。这里再补充下上面的推导过程用到的对数的法则:
总时间复杂度
好了,到此关键部分已经分析完了,下面综合上面的结论来看看总的时间复杂度。对于有 个节点的跳表,可以将查找过程分为两部分,一个是从第 层到最底层,另一个是从顶部到第 层。
从第 层到最底层,按照前面的等价逆向分享,相当于从底层往上爬 层,这里爬升的成本是:
接着是从顶部到第 层,这部分也是分为向左和向上。向左的步数最多也就是 层的节点数 。向上的话,从 LevelDB 的实现中,最高层次限制了 12 层,所以向上的步数也是一个常量。其实就算不限制整个跳表的高度,它的最大高度期望也可以计算出来(这里忽略计算过程,不是很重要):
所以不限制高度的情况下,这里的整体时间复杂度上限是:
上面的时间复杂度其实也就是 。最后再多说一点,虽然从第 L 层开始搜索比较好,但是实际实现中也没必要这样。像 LevelDB 一样,限制了整体跳表高度后,从当前跳表的最大高度开始查找,性能也不会差多少的。因为从第 L 层开始往上的搜索代价是常数级别的,所以没有大影响。此外,其实实现中最大层数也是根据 p 和 n 推算的一个接近 L 层的值。
P 值选择
论文中还分析了 p 值选择对性能和空间占用的影响,这里也顺便提下。显而易见,p 值越小,空间效率越高(每个节点的指针更少),但搜索时间通常会增加。整体如下表:
| p | Normalized search times (i.e., normalized L(n)/p) | Avg. # of pointers per node (i.e., 1/(1-p)) |
|---|---|---|
| 1/2 | 1 | 2 |
| 1/e | 0.94… | 1.58… |
| 1/4 | 1 | 1.33… |
| 1/8 | 1.33… | 1.14… |
| 1/16 | 2 | 1.07… |
论文推荐这里的 p 值选择 1/4,既有不错的时间常数,每个节点平均空间也比较少。LevelDB 中实现选择了 p = 1/4,Redis 的 zset 实现中也是选择了 ZSKIPLIST_P=1/4。
此外关于最高层数选择,LevelDB 中实现选择了 12 层,Redis 中选择了 32 层。这里是基于什么考虑呢?
回到前面的分析中,我们知道从一个合适的层开始搜索效率最高,这里合适的层是 。现在 p 已经确定是 1/4,只要能预估跳表的最大节点数 N,那么就能知道合适的层是多少。然后设置最大层数为这个值,就能保证跳表的平均性能。下面是 p=1/4 时,不同节点数对应的合适层数:
| 概率值 p | 节点数 n | 合适的层数(最大层) |
|---|---|---|
| 1/4 | 8 | |
| 1/4 | 10 | |
| 1/4 | 12 | |
| 1/4 | 16 | |
| 1/4 | 32 |
Redis 中选择了 32 层,因为要支持最多 2^64 个元素。LevelDB 中在 Memtable 和 SSTable 中用跳表存储 key,里面 key 的数量不会很多,因此选择了 12 层,可以最大支持 2^24 个元素。
性能测试 benchmark
LevelDB 中没有对跳表的性能进行测试,我们自己来简单写一个。这里用 Google 的 benchmark 库,来测试跳表的插入和查找性能。为了方便对比,这里也加了一个对 unordered_map 的测试,看看这两个的性能差异。跳表插入的测试核心代码如下:
1 | static void BM_SkipListInsertSingle(benchmark::State& state) { |
这里针对不同跳表和 unordered_map 表的长度,执行随机数字插入和查找,然后计算平均耗时。完整的代码在 skiplist_benchmark。注意这里 benchmark 会自动决定 Iterations 的次数,跳表插入每次初始化有点久,所以这里手动指定了 Iterations 为 1000。
./skiplist_benchmark –benchmark_min_time=1000x
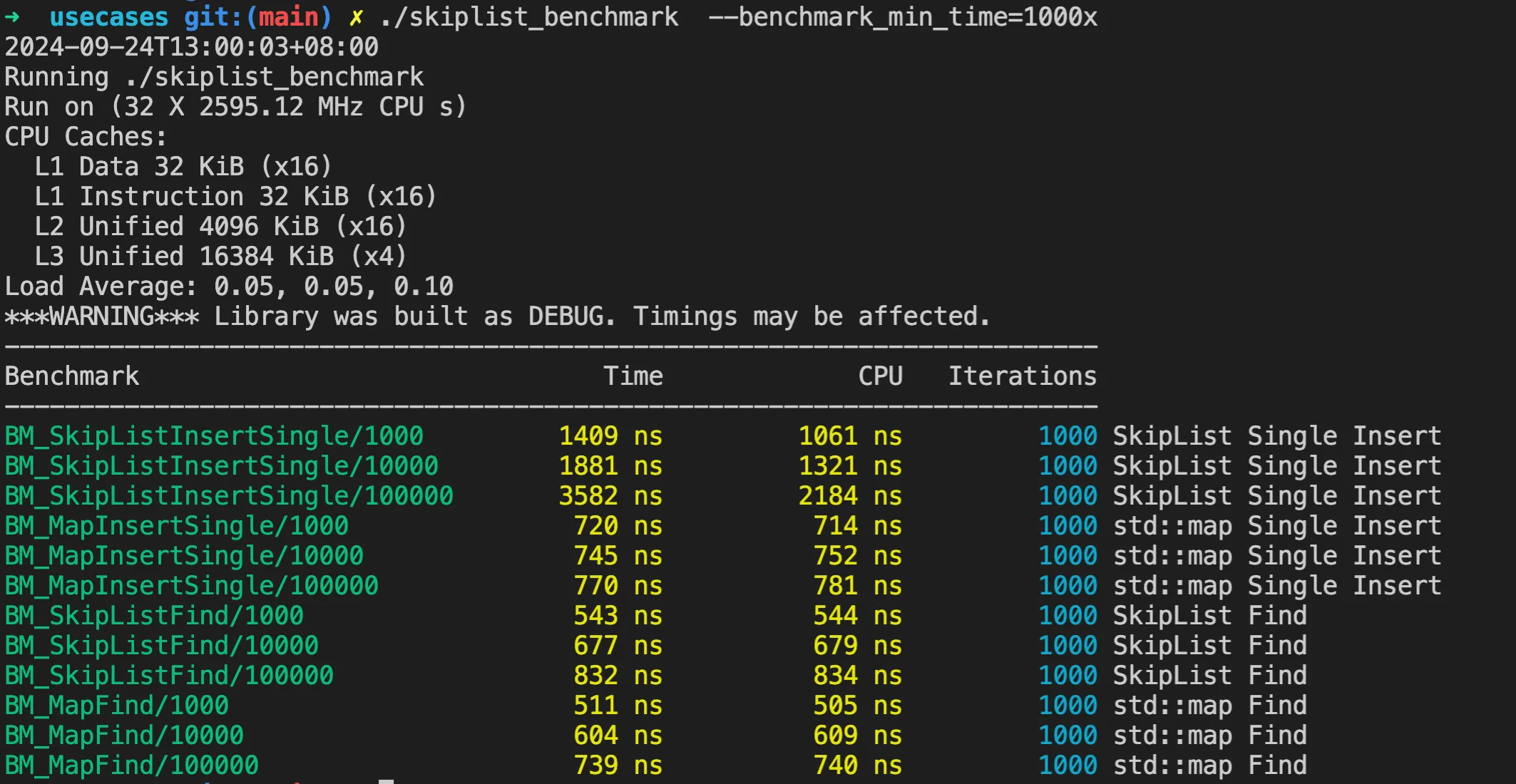
运行结果如下:
虽然这里是编译的 Debug 版本,没有优化。但是根据这里的测试结果可以看到,虽然跳表长度增加,但是插入耗时并没有显著增加。查找性能和 unordered_map 相比,差别也不是很大。
总结
本文是 LevelDB 跳表的最后一篇了,详细分析了跳表的时间复杂度。通过拆解查找问题,逆向整个查找过程,以及找到合适的 L 层,最后推导出跳表的时间复杂度。在知道时间复杂度的基础上,进而推导如何选择概率 p,以及 redis 和 LevelDB 中跳表的最大高度选择原因。最后通过简单的 benchmark 测试了跳表的性能,并与 unordered_map 进行了对比。
本系列其他两篇文章: